Making sense of graph databases part 4 - Why are graph databases more efficient than RDMS on connected data
Main article can be found here.
In a previous post, it was argued that graph databases are superior to RDMS on connected data because, RDMS has to do lots of joins. In this post we will look into why.
So, why are joins not a problem for Neo4j? The neat thing about Neo4j is that it does not use indexes at all. Instead, graph nodes are linked to its neighbours directly in the storage. This property of reference is called index-free adjacency. So, when Neo4j performs a graph query for retrieving a sub-graph, it simply has to follow the links in the storage – no index lookups are needed. The cost of each node-to-node traversal is O(1) – so if we are doing a friend-of-a-friend look-up to find, for example, all indirect friends of Alice, the total cost would be proportional to total number of friends in the final result – O(m) where m is the total number of Alice’s indirect friends. Even if the data (number of nodes) increases, if the total number of friends are still the same, the cost will still by O(m). This is because Neo4j first “jumps” to the Alice node using some kind of search or index, and then it simply visits the relating nodes by following the links, until the query is satisfied 1.
To compare the graph database approach with RDMS we will go through a simple example. In a previous post, join types used in the comparison below were examined, together with their algorithms, which the Big-O number used in this post are related to.
Assume that we have tables Employees (E), Departments (D) and Payments (P).
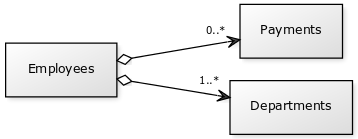
By joining E with D and then E with P, we can calculate for example sum payment for a given department. Given departments x and y, we want to find all the payments to its employees. By using nested loop join, this approach has a cost of O(2 * |E| * |P|) (2 for two departments, as we assume that an hash index is used to retrieve the x and y). Using hash join, this gives a cost of O(2 +|E|+2*|E|+|P|), where 2+|E| is the first join, and 2*|E|+|P| is the second. Again, the first 2 is for retrieving x and y, while |E| is for looping the larger table. 2*|E| is the number of maximum rows that can be constructed by joining x and y with E. The |P| is the final looping of each row to find corresponding employee in the first joined set, and to create joined rows.
A subset graph of this example is as follows:
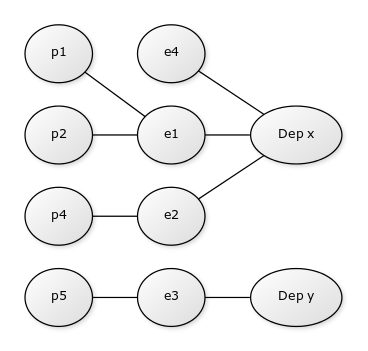
where e’s are employees and p’s are payments.
To find the payments with Neo4j, first a search is conducted to find the departments x and y. Using hash indexing this gives O(1). Then the graph is “walked” to find all the relevant payments, by first visiting all employees in the departments, and through them, all relevant payments. If we assume that the number of payment results are k, then, as mentioned in the Graph Database book 1, this approach takes O(k). We now have the following costs for our query:
- nested loop join:
O(|E| * |P|) - hash join:
O(|E|+|P|) - Neo4j:
O(k)
Two conclusions can be drawn from these:
- As the amount of rows increases in
EandP, the nested loop join and hash join cost will increase, while Neo4j cost is the same. If index are used to pinpoint the correct datasets, the database still needs to search the index. This takesO(log(n))for B+ trees, a number that also increases as the data is added, although slowly (in practice, the growth is often not a problem 2). Using hash index, this search may be reduced toO(1), but hash indexes are often difficult to scale, don’t support range queries and rebuilding indexes takes a lot of time 3, so B+trees are more common. Neo4j cost is not dependent of the amount of data, thus it stays the same. So, if millions of new rows were added to all the tables, both RDMS join approaches will suffer resulting in slower performance, while the graph database performance will be almost the same (except the first search after departmentxandy). - If we add more intermediary nodes in the graph, corresponding to new tables in the joins, both approaches suffer, but RDMS cost can increase non-linearly. As an example we can add a new table called PaymentItem (
PI) which describe some detail for a payment, and change our query to find payment items related to departments. The graph database would now have to “walk” a longer distance to perform the query, but because the graph database walk started from the correct departments, it will only consider the relevant payment items, instead of all. For RDMS, another table will be added to the joins and the cost change toO(2 * |E| * |P| * |PI|)for nested loop join, andO(2 +|E|+2*|E|+|P|+2*|E|*|P|+|PI|)for hash join. These cost are non-linear and much larger than for graph! Thus, adding new table relations in RDMS can result in non-linear performance increase in worst case.
Note that these conclusion describe the worst case and in practice, by tuning and optimizing, the cost for using RDMS can be heavily reduced.
Related Work
Analysis in this post is of course a very simple one, and was mostly conducted to understand the underlying details. In my research I did a survey find others say about Neo4j performance.
- Vicknair, Chad, et al. “A comparison of a graph database and a relational database: a data provenance perspective.” Proceedings of the 48th annual Southeast regional conference. ACM, 2010.
- This comparison between Neo4j and MySQL is from 2010 and shows that Neo4j performs well on queries involving graph traversals and text search. However, MySQL has performs similar to Neo4j on queries for orphan nodes, and outperforms Neo4j for queries involving integer payload (e.g. Count the number of nodes whose payload data is less than some value).
- https://baach.de/Members/jhb/neo4j-performance-compared-to-mysql/view
- This is also a comparison between Neo4j and MySQL where the author is examining the performance claims from 1 by redoing the queries from the book. Here, the author manages to get better results with MySQL than Neo4j on friend-of-a-friend graph, and he is unsure of why.
- De Abreu, Domingo, et al. “Choosing between graph databases and rdf engines for consuming and mining linked data.” Proceedings of the Fourth International Conference on Consuming Linked Data-Volume 1034. CEUR-WS. org, 2013.
- This is a performance comparison of graph databases DEX, Neo4j, HypergraphDB and RDF-3x where they conclude with that none of the graph databases are superior the other in all graph based tasks. Neo4j has
a better performance in BFS and DFS traversals, as well as in mining tasks against sparse large graphs with high number of labels.
- Martínez-Bazan, Norbert, et al. “Efficient graph management based on bitmap indices.” Proceedings of the 16th International Database Engineering & Applications Sysmposium. ACM, 2012.
- Here, the authors describe the internals of the graph database DEX and the clever usage of bitmap indexing in their graph model. In their experiments, DEX outperforms Neo4j on the queries they tested. More interesting is that, even MySQL outperforms Neo4j in their tests!
-
Robinson, I., Webber, J. & Eifrem, E. (2013). Graph databases. Sebastopol, Calif. Sebastopol, CA: O’Reilly Media,O’Reilly Media, Inc. ↩ ↩2 ↩3
-
Use the Index, Luke: The Search Tree (B-Tree) Makes the Index Fast: http://use-the-index-luke.com/sql/anatomy/the-tree ↩
-
Ramakrishnan, Raghu, and Johannes Gehrke. Database management systems. Boston: McGraw-Hill, 2003. slides from chapter 12 ↩